Diese Seite funktioniert nur mit Javascript.
Mathematische Herleitung der Kontraktkurve5.1.2 Die Produktions-BoxDie Transformationskurve

aben Sie die Konstruktionsweise der Edgeworth-Box einmal verstanden und sind sich über die Gleichgewichtsbedingung auf der Kontraktkurve im klaren, sollten Siw die Ausführungen in diesem Abschnitt leicht nachvollziehen können. Auf der Produktionsseite kommt nämlich genau dasselbe Instrumentarium zum Einsatz wie auf der KOnsumseite, also beim Tausch. Es ändern sich allein die Bezeichnungen. Der Übergang von der Tausch- zur Produktionsbox ist vergleichbar dem von Haushaltsgleichgewicht zur Minimalkostenkombination. Der einzige Unterschied besteht dort wie hier darin, dass sich das Ziel der effizienten Produktion (oder im dualen Problem der minimalen Kosten) nun im Gegensatz zum Nutzen kardinal messen lässt.
Aus den Konsumenten des vorigen Kapitels werden jetzt Produzenten. Wir gehen aus von einem Produzenten und einer Produzentin, die in zwei Betrieben unter Einsatz der Produktionsfaktoren Kapital K und Arbeit L Bier und Zigaretten produzieren ("2x2-Modell"). In einem Betrieb wird Bier und im anderen werden Zigaretten hergestellt. Die vereinfachenden Annahmen homogener, beliebig teilbarer Güter und fehlender Transaktionskosten gelten weiterhin.
Wir gehen davon aus, dass der Bier-Produzent und die Zigaretten-Produzentin verheiratet sind - der Grund folgt gleich- und derzeit jeweils fix vorgegebene Mengen an Kapital und Arbeit je Periode in ihren Betrieben beschäftigen. KB bezeichne dabei das in der Bierproduktion eingesetzte Kapital usw. Während der Betrachtungsperiode sei zwar der Gesamteinsatz von Kapital und Arbeit fest vorgegeben, doch sei andererseits die Aufteilung der Faktoreinsatzmengen zwischen den Betrieben ein Problem unseres Produzentenehepaares. Etwas eleganter formuliert: es geht um die Lösung des Allokationsproblems bei vollkommen unelastischem Faktorangebot. Wir suchen die optimale Faktorallokation.
Aus der Annahme, dass Produzent und Produzentin verheiratet sind, wird eine beiden gemeinsame Zielfunktion abgeleitet. Wären die beiden nicht verheiratet, dann müssten wir uns nämlich Gedanken machen, in welchem Verhältnis sie untereinander die beiden Produktionsfaktoren tauschen würden. Aus dem vorigen Abschnitt wissen wir jedoch, dass dieses Verhältnis unbestimmt ist, solange wir nur zwei (oder wenige) Personen betrachten. Sind sie jedoch verheiratet, unterstellen wir ihnen untereinander perfekt altruistisches Verhalten. Das Tauschproblem entfällt.
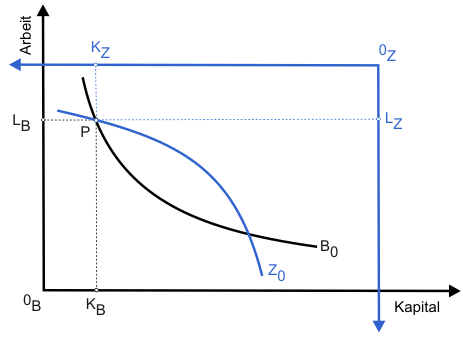
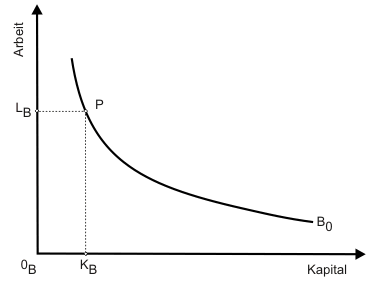
Bevor wir wieder mit einer bekannten grafischen Darstellung beginnen, schließen wir mit der letzten Annahme überlinear-homogene Produktionsfunktionen aus. Abbildung 1 zeigt eine Isoquante am Beispiel der Bierproduktion. Mit den Faktoreinsatzmengen KB und LB werden B0 Einheiten Bier hergestellt.
Machen Sie sich an dieser Stelle bitte klar, dass die Steigung der Isoquante die Grenzrate der technischen Substitution anzeigt, m.a.W. angibt, wie viel Einheiten Kapital bei Aufgabe einer Einheit Arbeit notwendig wären, um die Produktionsmenge konstant zu halten.
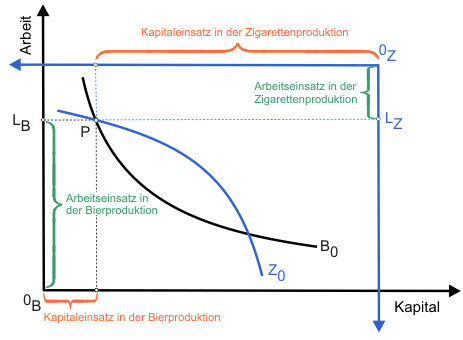
Vollkommen analog zur Abbildung 1 ließe sich ein Isoquantenschema für die Zigarettenproduktion zeichnen; alle Faktoren, die nicht in der Bierproduktion eingesetzt werden, sollen dort beschäftigt sein. Ebenso ließen sich vollkommen analog zur Vorgehensweise bei der Konstruktion der Tauschbox die beiden Diagramme in einer Box zusammenführen. Diese Box nennt man Produktions-Box. Sie ist in Abbildung 2 dargestellt. Ihre Kantenlänge zeigen den Bestand von Kapital und Arbeit an.
Wenn der Bier-Produzent und seine Zigaretten produzierende Gattin diese aktuelle Situation betrachten, können sie sich mithilfe eines kleinen Zahlenbeispiels leicht klarmachen, dass sie mit dem vorgegebenen Faktoreinsatz auch bessere Produktionsergebnisse erzielen können (oder "die Allokation nicht pareto-effizient ist" oder "gegen das ökonomische Prinzip verstoßen wird"). Für dieses Zahlenbeispiel seien folgende Werte für die physischen Grenzproduktivitäten angenommen:
| Bier- produktion | Zigaretten- produktion | |
| Arbeit | 4 | 9 |
| Kapital | 2 | 3 |
Werden nun aus der Zigarettenproduktion 3 Einheiten Kapital abgezogen, dann muss 1 Einheit Arbeit mehr beschäftigt werden, um die Produktion konstant zu halten. In der Bierproduktion jedoch werden für den Ersatz dieser Einheit Arbeit nur zwei Einheiten Kapital benötigt. Die Produktionsmengen beider Güter können also auch mit einer Einheit Kapital weniger erzeugt werden. Quintessenz: in der Ausgangssituation werden Produktionsfaktoren verschwendet.
Grafisch erkennt man die nicht effiziente Situation an den sich schneidenden Isoquanten, d. h. an unterschiedlichen Grenzraten der technischen Substitution in den Produktionen von Bier und Zigaretten. Diese unterschiedlichen Grenzraten sind auch im Zahlenbeispiel angenommen, da die Grenzrate der technischen Substitution dem (negativen, umgekehrten) Verhältnis der Grenzproduktivitäten entspricht. Nebenbei: die physischen Grenzproduktivitäten müssen, um technisch effiziente Allokation zu gewährleisten, in verschiedenen Verwendungen eines Faktors nicht gleich sein. Sie lassen sich ja auch gar nicht miteinander vergleichen, denn was hätte man denn von einer Information, dass die Grenzproduktivität der Arbeit bei der Produktion von Schlagsahne und Backsteinen jeweils 2 betrüge? Es gilt aber, dass bei Gewinnmaximierung der Ausgleich der Wertgrenzproduktivitäten zwischen verschiedenen Verwendungen notwendige Bedingung ist, wenn der Faktoreinsatz effizient sein soll. Wenn das nicht der Fall wäre, würde es sich lohnen, den Faktor in die Produktion umzuleiten, bei dem er das höhere Wertgrenzprodukt erbringt.
Haben Produzent und Produzentin einmal die ineffiziente Faktorallokation erkannt, werden sie sich überlegen, in welcher Weise die Faktoren zu alloziieren sind, so dass die Verschwendung von Ressourcen unterbleibt. Analog zu den Überlegungen zur Tauschbox kann die Produktion beider Güter augenscheinlich durch eine Bewegung von Punkt P in Abbildung 2 aus in die Linse erhöht werden. Die Produktion von Bier wird dabei kapitalintensiver, die von Zigaretten arbeitsintensiver, d.h. Kapital wird von der Zigaretten- in die Bierproduktion und Arbeit von der Bier- in die Zigarettenproduktion gelenkt.
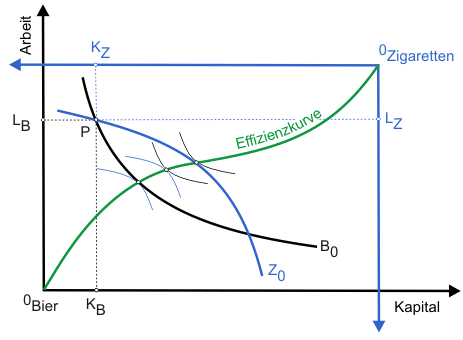
Die Allokation der Faktoren ist effizient, wenn auf der sogenannten Effizienzkurve produziert wird, die der Kontraktkurve in der Tauschbox entspricht.
Wie in der Tauschbox wissen wir an dieser Stelle noch nicht, welchen Punkt auf der Effizienzkurve das Produzentenehepaar wählen wird. Im Gegensatz zur Theorie des Tausches sind wir hier jedoch in der Lage, diesen Punkt zu bestimmen, wenn wir dem Ehepaar Gewinnmaximierung unterstellen und die Marktpreise von Bier und Zigaretten kennen (wir kommen darauf bei der analytischen Herleitung zurück). Unter den getroffenen Annahmen (insbesondere Homogenität der Produktionsfunktionen) existiert immer eine eindeutige gewinnmaximale Lösung, wenn die Produktionsfunktionen für beide Güter nicht trivialerweise identisch sind.
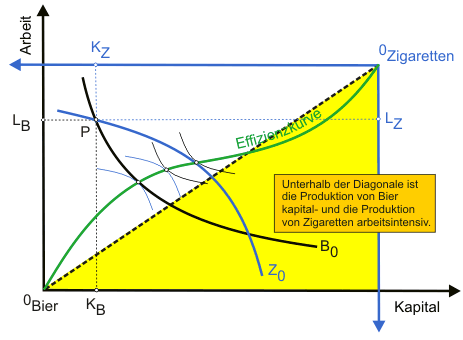
Zwar wird die Effizienzkurve häufig so wie in Abbildung 3 eingezeichnet, wo sie die Diagonale der Box schneidet, jedoch wird diese Möglichkeit andererseits ebenso häufig per Annahme ausgeschlossen. Der Grund ist folgender: In allen Punkten auf der Effizienzkurve, die oberhalb der Diagonalen liegen, ist die Produktion von Bier relativ arbeitsintensiv. Schneidet die Effizienzkurve die Diagonale von oben nach unten, so wird Bier zum kaptalintensiv und die Zigaretten zum arbeitsintensiv produzierten Gut. Anwendungen der Theorie des Allgemeinen Gleichgewichts (vor allem in der Theorie des Außenhandels) werden in einem solchen Fall kompliziert. So gesehen ist klar, warum man die ausschließende Annahme trifft. Ob sie der Realität gerecht wird, ist eine andere Frage.